S využítím Sylvesterových matic lze lineární polynomiální maticové rovnice elegantně přepsat do tvaru lineárních rovnic s konstantami, které lze pak řešit s pomocí existujících silných algoritmů a programových balíků pro problémy lineární algebry (LAPACK, MATLAB apod.). Takto vzniklé rovnice jsou navíc silně strukturované, čehož bychom chtěli využít.
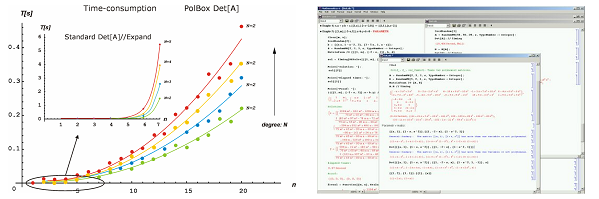
První možnou cestou k dosažení tohoto cíle je použití solverů pro pásové matice. Výhodou je existence příslušných solverů např. v balíku LAPACK, jehož funkce lze poměrně snadno volat z MATLABu a Polynomiálního toolboxu, na kterém pracujeme. Nevýhodou je pak skutečnost, že strukturu problému využijeme pouze částečně, nevyužíváme ji zcela. Naznačený postup jsme naprogramovali ve formátu prototypového programu pro Polynomial Toolbox a dosahujeme úspory výpočetního času až 80% pro polynomy vysokých stupňů. Kontakt: Martin Hromčík
Náročnější cestou je pak vývoj skutečně dedikovaných algoritmů, od začátku do konce, s uvážením veškerých souvislostí původního polynoiálního zadání a vzniklé konstantní soustavy. Vzniklé metody využívají modifikací obratů známých z moderní lineární algebry jako jsou Givensovy rotace nebo Householderovy transformace. V současnosti pracujeme na efektivní implementaci těchto nových metod a těšíme se na jejich praktické srovnání s výše zmíněným postupem. Kontakt: Didier Henrion