O skupině
Náš tým vytváří nové originální postupy pro počítání s polynomy (mnohočleny) a maticemi polynomů a také pro řešení rovnic s polynomy a maticemi polynomů s cílem aplikovat je v systémech, signálech a řízení. Zatímco teorie využití polynomů a jejich matic např. pro návrh systémů a jejich řízení je dnes rozšířena po celém světě, dostatečně rychlé a spolehlivé algoritmy pro takové výpočty donedávna chyběly a proto do praxe pronikly polynomiální metody teprve v minulé dekádě.
Protože jsme v této oblasti dosáhli velkého pokroku, je v ní náš tým všeobecně považován za vedoucí skupinu na světě. Vyvinuli jsme mnoho originálních metod: nejprve velmi spolehlivé metody založené na Sylvestrových maticích - dnes jim říkáme "metody druhé generace" a nedávno stejně spolehlivá avšak navíc mnohem rychlejší metody používající interpolaci a rychlou Fourierovu transformaci FFT - to jsou "metody třetí generace".
Nové metody publikujeme ve špičkových mezinárodních časopisech. Takových článků členům našeho týmu již vyšlo několik desítek. Největším publikačních úspěchem jsou tři články otištěné v nejlepším časopisu oboru, americkém IEEE Transactions on Automatic Control v prestižní kategorii "velký článek". Naše publikace jsou po celém světě hojně citovány. Řídíme evropskou síť excelence výzkumných pracovišť a firem pro průmyslové aplikace polynomiálních metod EUROPOLY a mnoho mezinárodních i národních projektů v této oblasti.
Vyvinuté algoritmy nejen matematicky dokazujeme a vědecky publikujeme, ale každou samozřejmě intenzivně testujeme experimentálně a ve formě prototypových programů předáváme do průmyslu. Například česká firma PolyX s.r.o. je implementuje ve svém komerčním produktu Polynomial Toolbox for Matlab. Naše algoritmy tak úspěšně používají koncoví průmysloví uživatelé Polynomiálního Toolbox po celém světe, a to jak velké podniky, např. Lockheed Martin, SANDIA National Lab a National Instruments, (vše USA); Mitshubishi Electric, J; Petrobras, BRA, Saudi Armaco, SA, QuinetiQ, GB, tak i malé hi tech firmy Compureg, CZ, ProCS, SK a Cybernet Systems Ltd., J.
 |
K čemu to je
V oboru systémů, signálu a řízení stále častěji počítáme nikoli s čísly, ale se složitějšími objekty, např. s polynomy. Tak třeba když k soustavě (tj. systému, který máme řídit, např. průmyslovému procesu, raketě, lodi, automobilovému motoru, ruce robota, lidskému svalu, ...) s přenosem b(s)/a(s) připojíme do zpětné vazby regulátor s přenosem y(s)/x(s), jsou vlastnosti a chování výsledného systému popsány výrazem
![]()
Protože nejčastěji všechny a(s),b(s),x(s),y(s) jsou polynomy v proměnné s, tak je polynomem i výsledné c(s) na pravé straně. Přitom matematické vlastnosti polynomu dobře vyjadřují technické vlastnosti skutečného výsledného systému (např. dynamika, rychlost, stabilita, vibrace, tlumení, citlivost na změny nebo poruchy,...). Inženýr z našeho oboru často řeší opačný problém: zákazník (majitel reálného systému popsaného tím b(s)/a(s)), s ním není spokojen a přeje si změnit jeho vlastnosti a chování. Nejlepším řešením je často řídící systém (regulátor), který pracuje ve zpětné vazbě (tj. měří chování - výstup - dané soustavy a podle toho, co naměří, vytvoří vhodný zásah - vstup do soustavy - tedy jí řídí. Pokud se nám podaří vtělit požadavky zákazníka do vlastností polynomu, pak přenos hledaného regulátoru y(s)/x(s)snadno zjistíme z výše uvedeného výrazu. Pro dané polynomy a(s),b(s),c(s) ho vyřešíme jako polynomiální rovnici s neznámými polynomy x(s),y(s). Jakmile najdeme vhodné řešení, je už hračkou vypočtený regulátor realizovat a k soustavě připojit. Úspěch přirozeně také závisí na tom, jak dobře (přesně, spolehlivě a rychle) dokážeme tu rovnici vyřešit.
Systémy, které dnes musíme řídit, jsou často mnohem složitější. Třeba proto, že mají mnoho výstupních a vstupních signálů. U nich se setkáme s trochu složitějšími rovnicemi
![]()
kde všechny objekty jsou matice polynomů, například něco jako
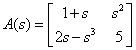
Řešit rovnice s maticemi polynomů je samozřejmě těžší. Konečně mohou být náročnější i požadavky zákazníka na řídicí systém. Ten často chce, aby výsledný systém byl optimální (choval se co možná nejlépe) a/nebo robustní (choval se rozumě, i když je popis původní systému velmi nepřesný, když se původní systém mění apod.) Pak musíme řešit ještě složitější rovnice, třeba kvadratické, jako například
![]()
nebo maticovou
![]()
V reálných situacích potkáváme stále složitější systémy, a proto je řešení výše uvedených rovnic i další výpočty či operace a manipulace s polynomy i jejich maticemi i pro počítače stále náročnější. Proto je třeba hledat a vyvíjet stále efektivnější algoritmy a metody.
Kdo financuje náš výzkum
Náš výzkum je průběžně financován z různých průmyslových a státních projektů. V minulosti např. z evropských projektů Copernicus Project CP93:2424: Algorithms for CAE Based on Modern Polynomial Design Methods in Control a Copernicus Project CP97:7010 EUROPOLY – The Network of Excellence for Industrial Applications of Polynomial Methods (který vedoucí našeho týmu dokonce koordinoval) a projektu NATO PST.CLG.978481 Computer Algorithms for Polynomial Methods in Signals and Systems. Dále z dvoustranných mezinárodních projektů česko-francouzských (Barrande 97026), česko-japonských (NJ 11/98), česko-italských (NT1-25), česko-rakouských (AKTION) a česko-řeckých (12-00). V současné době tento výzkum podporuje projekt Centrum aplikované kybernetiky (MŠMT 1M0567) a grant GAČR (102/05/0011).


